Using the (3N)-dimensional generalized Lorenz systems as a testbed for data assimilation: The ensemble Kalman filter
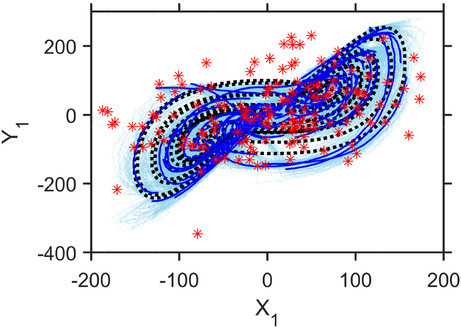 Solution trajectories of the true solution (black dotted), assimilated ensemble members (cyan solid), and the ensemble mean (blue solid) along with observations (red asterisks) showing that too many inaccurate observations can ruin the data assimilation process.
Solution trajectories of the true solution (black dotted), assimilated ensemble members (cyan solid), and the ensemble mean (blue solid) along with observations (red asterisks) showing that too many inaccurate observations can ruin the data assimilation process.
Abstract
The feasibility of using a (3N)-dimensional generalization of the Lorenz system in testing a traditional implementation of the ensemble Kalman filter is explored through numerical experiments. The generalization extends the Lorenz system, known as the Lorenz ’63 model, into a (3N)-dimensional nonlinear system for any positive integer N. Because the extension involves inclusion of additional wavenumber modes, raising the dimension allows the system to resolve smaller-scale motions, a unique characteristic of the present generalization that can be relevant to real modeling scenarios. Model imperfections are simulated by assuming a high-dimensional generalized Lorenz system as the true system and a generalized system of dimension less than or equal to the dimension of the true system as the model system. Different scenarios relevant to data assimilation practices are simulated by varying the dimensional differences between the model and true systems, ensemble size, and observation frequency and accuracy. It is suggested that the present generalization of the Lorenz system is an interesting and flexible tool for evaluating the effectiveness of data assimilation methods and a meaningful addition to the portfolio of testbed systems that includes the Lorenz ’63 and ’96 models, especially considering its relationship with the Lorenz ’63 model. The results presented in this study can serve as useful benchmarks for testing other data assimilation methods besides the ensemble Kalman filter.