Coexisting attractors in a physically extended Lorenz system
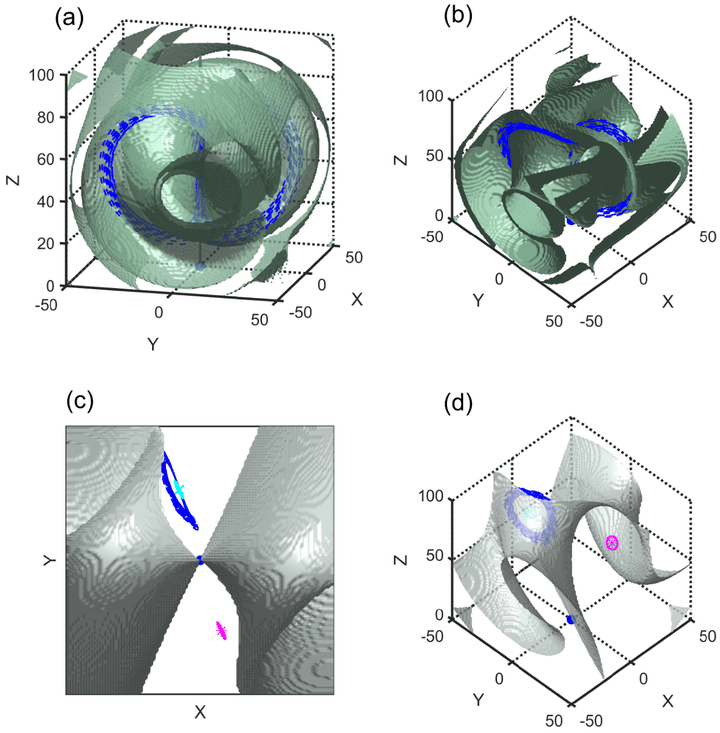 Basin boundaries in a 3D phase space
Basin boundaries in a 3D phase space
Abstract
Coexisting attractors may arise from many different sources such as hidden basins of attraction or peculiarly organized bifurcation structures. By exploiting the regions of mismatched bifurcations between the system and its fixed points, this study investigates coexisting attractors in a six-dimensional extension of the Lorenz system. This six-dimensional extension takes into account additional physical ingredients, namely, rotation and density-affecting scalar, which are not considered in the original Lorenz system. These newly considered physical ingredients can influence the bifurcation structures and thus the system’s characteristics with regard to coexisting attractors. Once the potential regions of coexisting attractors are identified in the parameter spaces, the coexistence of periodic and point attractors and that of two different periodic orbits in addition to the well-known coexistence of chaos and stability are demonstrated through the solution trajectories and attractor basin boundaries.