Increasing model vertical resolution may not necessarily lead to improved atmospheric predictability
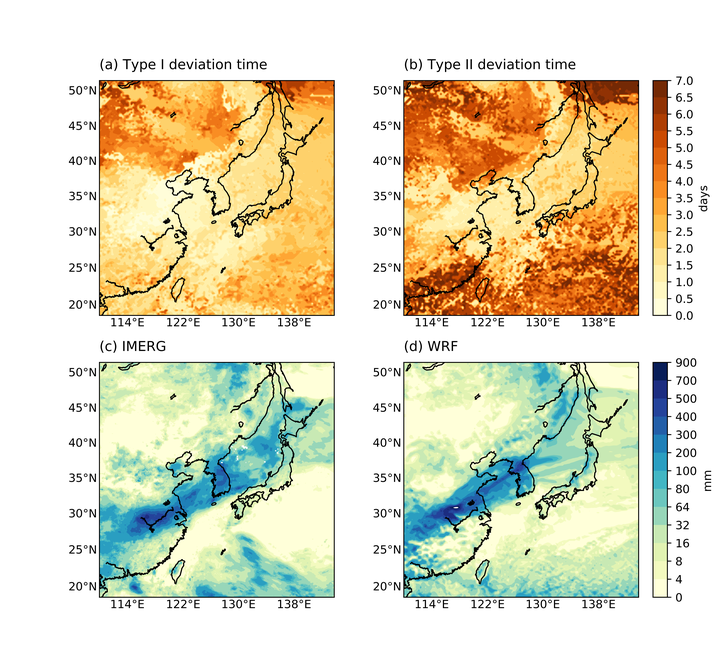 The two types of deviation times along with IMERG satellite data and WRF simulation results with 40 model levels.
The two types of deviation times along with IMERG satellite data and WRF simulation results with 40 model levels.
Abstract
The widely accepted existence of an inherent limit of atmospheric predictability is usually attributed to weather’s sensitive dependence on initial conditions. This signature feature of chaos was first discovered in the Lorenz system, initially derived as a simplified model of thermal convection. In a recent study of a high-dimensional generalization of the Lorenz system, it was reported that the predictability of its chaotic solutions exhibits a non-monotonic dimensional dependence. Since raising the dimension of the Lorenz system is analogous to refining the model vertical resolution when viewed as a thermal convection model, it is questioned whether this non-monotonicity is also found in numerical weather prediction models. Predictability in the sense of sensitive dependence on initial conditions can be measured based on deviation time, that is, the time of threshold-exceeding deviations between the solutions with minute differences in initial conditions. Through ensemble experiments involving both the high-dimensional generalizations of the Lorenz system and real-case simulations by a numerical weather prediction model, this study demonstrates that predictability can depend non-monotonically on model vertical resolution. Further analysis shows that the spatial distribution of deviation time strongly contributes to this non-monotonicity. It is suggested that chaos, or sensitive dependence on initial conditions, leads to non-monotonic dependence on model vertical resolution of deviation time and, by extension, atmospheric predictability.